太原理工大学|周文晋,张雅桐,赵志仝,张玮:功热集成中压力操作路径和换热匹配的同步优化
功热集成中压力操作路径和换热匹配的同步优化
周文晋
张雅桐赵志仝张玮
（太原理工大学化学与化工学院，山西 太原 030024）
DOI：10.11949/0438-1157.20250743
摘 要传统的功热网络优化设计方法往往先确定变压过程，随后进行换热网络设计。基于超结构的功热网络同步优化方法因其能考虑功热间的耦合与相互影响，可实现更优的系统整体性能。然而，此类同步优化模型通常高度非凸非线性，导致求解困难，尤其是面向大规模工业问题时。为应对这一难题，本研究提出了一种基于动态运输模型的确定性优化设计方法。该方法利用运输模型的特性，在保证热集成模型线性约束下，实现最优功热集成下系统压力操作路径与换热匹配方案的高效确定，并为功热网络的详细设计提供指导。针对一个包含14条换热流股的功热集成案例进行研究，提出的方法在1000 s内得到了一个新的压力操作路径以及相应的换热匹配，该方案的总费用目标值为8761480.49 USD·a-1，与文献中已知费用最优解高度逼近，验证了所提方法的准确性和有效性。关键词功热集成；数学规划；动态运输模型；优化设计；过程系统引用本文：周文晋, 张雅桐, 赵志仝, 张玮. 功热集成中压力操作路径和换热匹配的同步优化[J]. 化工学报, 2025, 76(12): 6477-6485(ZHOU Wenjin, ZHANG Yatong, ZHAO Zhitong, ZHANG Wei. Simultaneous optimization of pressure operating path and heat exchange matches in work and heat integration[J]. CIESC Journal, 2025, 76(12): 6477-6485)
引 言
功和热是化工过程中最普遍的两种能源形式，在工业对能源需求的持续增长背景下[1]，同时的功热集成能够有效提高能源的利用效率，从而得到了众多学者的关注。功热集成可看作传统过程集成方法的拓展[2]，通过协同回收过程变温变压流股的功和热量提高过程的能源利用效率，减少外部加热、冷却公用工程和电力的使用，实现化工过程的低碳可持续发展。传统的化工设计方法采用顺序设计流程，先基于工艺特点确定压力操作路径和变压单元配置，再进行过程流股的热集成。但这忽略了功和热的内在关联性，例如，变压单元的进口温度会同时影响功量和换热。在设计阶段考虑功和热的协同以及二者之间的权衡，相比顺序设计可以得到更优的结果。过程热集成和换热网络综合的研究目前已十分成熟，主要包括热力学设计方法[3]和数学规划方法[4]。基于超结构的数学规划方法由于能够协同考虑换热网络操作和投资费用的权衡，并且可以考虑其他非热力学因素，目前广泛用于换热网络的同步综合。化工过程通常包括一系列变压过程，对应的功集成有间接和直接两种形式[5]。间接功集成是基于高压流股通过透平或膨胀机做功产电，并为低压流股的增压过程提供电力实现。直接功集成则是将不同的变压单元集成到同一个轴机上来减少能量损耗，例如单轴透平压缩(single shaft turbine compressor, SSTC)设备[6]。热集成仅关注流股的温度变化，但功热集成中流股的压力和温度都是变化的，因此是一个非常复杂的集成问题。功热集成和功热交换网络(work and heat exchange network, WHEN)设计近些年来受到学者们的重视。早期的关键工作包括基于拓展的夹点方法与㶲分析的结合研究。Gunderson等[7]基于㶲效率准则提出了压缩机和膨胀机的放置规则。Wechsung等[8]基于数学规划法进一步拓展该方法，提出了低于环境温度工艺过程最小化不可逆性的设计工具。关于WHEN的同步综合，Onishi等[9]首次将换热网络多级超结构进行拓展[10]，考虑变压过程的同步设计，提出了相应的混合整数非线性优化模型。Huang等[11]基于拓展的多级超结构构建了功热集成的同步超结构模型[12]。Nair等[13]在WHEN同步综合中进一步考虑了流股的变压和冷热属性优化以及流股相变过程，并应用于离岸天然气液化过程。截至2019年的功热网络研究进展可参考Yu等[14-15]的综述。换热网络综合已被证明是NP难问题[16]，求解难度随问题规模非线性增加，功热网络的同步优化则进一步增加了问题的复杂程度。为有效解决功热网络的同步综合，2020年，Pavão等[17]提出结合夹点和超结构的优化框架，并使用双层元启发算法实现过程的设计，Santos等[18]在此基础上提出一种决策变量降维方法减少同步综合难度。2021年，Lin等[19]提出一种结合夹点和全局搜索的两步综合方法，并将其拓展为考虑环境和经济的双目标优化[20]，随后在流股单次换热和变压的最小结构假设基础上提出了基于枚举的确定性全局最优设计方法[21]。2024年，Lin等[22]基于单峰原则提出针对WHEN换热非最小结构的高效设计方法。此外，Zhuang等[23]提出改进的超结构，实现考虑多公用工程的功热集成综合问题。2024年，Ibrić等[24]提出一种两阶段的数学优化方法。2025年，Rossato等[25]提出结合夹点法和粒子群优化的双层算法，并基于分段线性化方法考虑严格的流股热力学性质。对于考虑多级变压操作和换热属性优化的WHEN同步设计问题，由于其优化问题的高度非凸非线性，目前依然缺乏稳定高效的设计方法。前人的研究多采用结合夹点和超结构的顺序两步综合方法，然而夹点法无法在目标确定阶段考虑换热匹配的确定和相关约束，并且通常难以精确确定综合费用目标值。因此，本研究提出基于运输模型的方法实现功热集成中压力操作路径和换热匹配的同步确定，为高效实现WHEN的近最优设计提供一种新方法。对于功热网络集成设计中同时确定最优压力操作路径和换热匹配的问题定义如下：给定一系列过程流股，它们的初始以及目标温度压力均已知。考虑使用压缩机和膨胀机对过程流股进行变压操作，使用换热器进行流股间的热量回收，达到目标温度需要的额外换热负荷通过冷热公用工程完成。目标是在功热网络设计前确定出合适的变压路径以及过程中冷热流股的匹配方式，以最小化网络的总费用。随后，基于前述信息可以构建精简的功热网络优化超结构模型，以高效稳定地确定整体功热网络的全局最优或近最优配置。（3）所有变压单元基于SSTC进行功集成，若总功量出现盈余则将其用于发电机发电，若总功量出现亏损则通过电动机消耗电能弥补，从而维持SSTC系统的功平衡；（6）变压单元为等熵过程，并且效率和多变指数已知；功热集成优化中，部分学者[5,10]在变压操作优化中考虑多级变压操作，并且每一级考虑变压单元类型的选择[26]，但这会增加优化问题的复杂度，并造成变压路径过于复杂和不切实际，并且从热力学的角度来看同时考虑加压和减压操作可能造成更低的系统不可逆性[27]。因此，本研究基于变压过程流股的初始和目标压力直接确定采用的变压单元类型，如图1所示，如果流股的初始压力(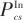
)小于目标压力(
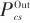)，则使用压缩机，需要优化压缩机的级数以及每个压缩机的进出口温度和压力，反之则使用膨胀机。图1低压流股多级压缩过程示意图Fig.1Schematic diagram of multi-stage compression process for low-pressure stream变压单元的进出口温度是需要优化的，因此这些换热流股的冷热属性无法直接确定。对于多级变压过程，为了在保持模型换热和功两方面充分权衡的基础上避免过于复杂的结构可能性，仅考虑在变压前和最终变压后流股的冷热属性优化，而对于级内换热流股，基于其使用的变压单元直接确定其换热属性。对于压缩过程，级间换热流股仅考虑冷却，而膨胀过程级间仅考虑加热。基于上述提出的启发式规则构建如图2所示的功热集成优化超结构示意图，包含加压流股和减压流股各一条以及两级变压操作。中间部分为热集成模块，可以通过超结构法建立对应的换热网络优化模型，也可以采用动态运输模型建立热集成优化模型，实现费用目标值的确定并获得合适的变压路径、流股冷热属性和换热匹配。图2提出的功热集成优化超结构示意图Fig.2Schematic diagram of proposed work-heat integration optimization superstructure对于流股变压级数和配置的确定采用基于析取规划的优化建模方法[28]。某一级压缩过程如式(1)所示。当压缩机存在时 (
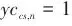)，左侧析取项被激活，其中包括压缩单元进口温度(
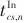)、出口温度(
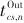)和压比(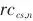
)的关联式，压比定义式以及压比的范围限制。当压缩机不存在时(
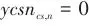)，右侧析取项被激活，该级的进出口温度和压力相同。类似地，膨胀流股在某一级变压过程的优化采用式(2)。 | 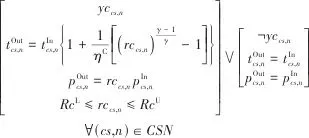 | (1) |
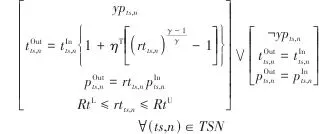|  | (2) |
式中，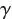
表示流股热容比，
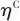和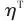
分别为压缩过程和膨胀过程的等熵效率。压缩过程和膨胀过程对应的功分别采用式(3)和式(4)计算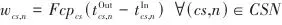： |  | (3) |
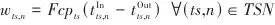|  | (4) |
式中，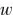
表示流股在某一级对应的压缩功或膨胀功，
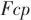表示流股的热容流率。功过程额外的约束则包括式(5)~式(10)，表示变压单元间以及与过程流股的温度和压力等式关联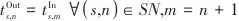： |  | (5) |
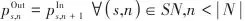|  | (6) |
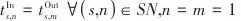|  | (7) |
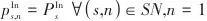|  | (8) |
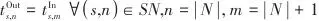|  | (9) |
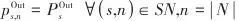|  | (10) |
SSTC系统中额外电动机和发电机对应的功分别通过式(11)和式(12)计算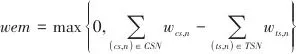： |  | (11) |
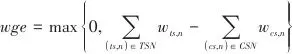|  | (12) |
另外，如果非第一级的变压流股不存在，则相邻后面的换热级的换热过程也不存在，采用式(13)和式(14)约束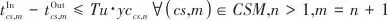： |  | (13) |
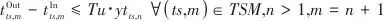|  | (14) |
传统功网络同步热集成优化采用拓展的组合曲线法或夹点定位法。这些方法都是基于夹点理论的方法，可以用于确定公用工程目标值并粗略估计总换热成本，但无法考虑流股的换热匹配。因此，本研究提出基于换热运输模型的同步热集成方法，直接考虑冷热流股间的热量分配，可以实现费用目标值的准确估计，并且直接获得对应的换热匹配。运输模型如图3所示。图3运输模型示意图Fig.3Schematic diagram of transportation model运输模型的建立基于对温度区间进行离散化处理，并考虑冷热流股在温度子区间内的热量直接传递，从而实现约束的线性化。本研究对传统的运输模型进行了改进，通过自适应温度区间构建使运输模型能够准确地预测换热网络总费用和确定合适的换热匹配。传统运输模型假定过程流股的进出口温度和热容流率均为常数，但功网络中换热流股的进出口温度是需要优化的变量，传统运输模型并不直接适用。因此对传统运输模型进行拓展，提出一种动态运输模型，使其能同时考虑流股的属性和温度优化，优化模型已在本课题组的相关工作[29]中详细阐述，限于篇幅，本节仅展示其关键约束和目标函数。析取式(15)表示对任一过程流股换热属性的自动识别，如果其进口温度大于出口温度则为热流股，否则为冷流股。 | 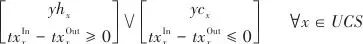 | (15) |
对于换热流股，由于进出口温度不确定，考虑其与运输模型温度子区间k的动态映射关系。如图4所示，主要包括3种映射：热流股温度范围大于温度子区间范围（情景1）、在温度子区间范围内（情景2）以及小于温度子区间范围（情景3）。相应的约束条件可以通过析取式(16)表示。同理可以建立冷流股的进出口温度和温度子区间的映射关系。图4温度区间k与热流股温度范围的相对位置关系Fig.4Relative position of temperature interval k and temperature range of hot stream | 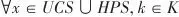 | (16) |
其他约束条件包括运输模型的热量平衡、换热面积计算、功网络模型和运输模型中变量的关联约束、变量边界等。功热网络的总年度费用包括功网络的费用和基于运输模型的换热网络费用，由式(17)计算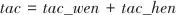： |  | (17) |
功网络费用包括辅助电动机运行费和发电机的收益以及包括压缩、膨胀、辅助的电动机和发电机单元的投资费[式(18)]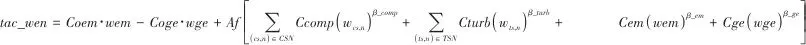： |  | (18) |
运输模型的总费用通过式(19)计算，其中第一项和第二项分别表示冷热公用工程的费用，第三项和第四项分别表示换热投资的固定项费用和可变量费用。 | 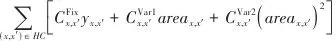 | (19) |
式中，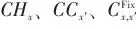
分别表示热公用工程、冷公用工程、换热器投资固定项费用系数，
、
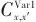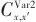表示可变项费用系数，
、
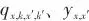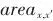分别表示冷热流股在可行换热子区间的换热量、换热匹配是否存在、换热匹配对应的换热面积估计。建立的功热同步集成优化模型以最小化总年度费用为目标函数，其中换热网络的费用基于提出的动态运输模型估计。模型中的析取规划和max操作符通过凸包重构转化为等价的代数方程约束，最终建立的优化模型为混合整数非线性规划问题，通过GAMS平台编程，使用全局优化求解器Gurobi求解。本研究提出的功热集成方法验证算例为火力发电燃烧后的碳捕集过程。如图5所示，采用两级膜分离工艺过程对CO2和N2进行分离[30]。该工艺过程包含4条变压流股，膜分离进口和渗余侧的压力为8 bar（1 bar=0.1 MPa），渗透侧和进料压力为1 bar，这些流股的进出口温度均为25℃。此外还有非变压的燃料气和空气流股可以进行热集成。Fu等[30]基于夹点法对该过程进行功热集成改造，减少了过程的功耗，充分实现该过程的功热集成以及实现功量和热量的回收。该算例的流股数据与其他参数见表1和表2，其中最大求解时间设置为1000 s。图5用于碳捕集的两级膜分离工艺Fig.5Two-stage membrane separation process for carbon capture表2其他参数Table 2Other parameters
该算例考虑变压级数最多为2级，一共包括14个换热流股，其中有8个换热属性未定的流股。该问题属于文献中较为复杂的功热集成算例，由于功网络的非凸性和问题规模较大，全局优化算法未能在给定时间内收敛，但相对最优性误差仅为5.8%，处于可接受范围。优化得到的功热网络总年度费用为8761480.49 USD·a-1, 对应的功网络变压单元进出口温度和压力优化结果如图6所示，两个加压流股选择使用单级压缩，减压流股选择使用两级膨胀。这样的结果是合理的，因为膨胀机的投资成本较低，选择多级膨胀带来的额外产功收益可以弥补投资的成本，而压缩机则因为投资成本较高，最优结果选择了最少的压缩级数。SSTC使用一个5908.83 kW的马达弥补不足的功率。优化结果中，压缩过程的换热流股的属性均为热流股，膨胀过程初始为等温流股，后续两端的属性为冷流股，这也符合减少过程的功耗。注意膨胀过程初始换热流股的温度偏差是方法中运输模型离散化区间设置的允许误差导致的。基于同步优化得到的换热匹配结果见表3，运输模型预测的换热网络总年化费用和换热总面积分别为2169357.07 USD·a-1和8076.39 m2。图6功网络优化结果Fig.6Optimization results of work network表3优化确定的换热匹配Table 3Heat exchange matches determined through optimization
本研究提出的功热集成方法得到的优化结果以及与文献的结果对比见表4。优化后，通过过程流股的热量回收，仅需要使用冷公用工程。本研究基于动态运输模型得到的费用目标值低于目前文献中的设计结果，并且得到了包含6个变压单元的新功网络设计方案，相比文献中的最佳设计结果多了3个换热匹配以及1个变压设备。变压设备和换热器数量有所增加，虽然导致投资费用进一步增加，但系统公用工程消耗和电耗的降低足以弥补这部分投资费用，整体费用预计会下降1.8%左右。文献中使用的是随机优化算法，本研究中的费用目标值结果证明了文献中结果的近最优性，也说明该问题的复杂性导致存在众多近最优解，得到全局最优解是十分有挑战性的。值得注意的是，该方案在结构上呈现出较高的复杂性，具体表现为变压单元从文献中最多的5个增加到6个，换热器数量也达到了12个，这种复杂性的提升是功热集成系统追求极致经济性的结果，由于设计得到的网络结构较为复杂，后续须进一步对经济性和网络可靠性进行权衡，从而在概念设计阶段得到更合理的设计结果。相比文献中的方法，本研究提出的方法可以为基于超结构法的功热网络同步设计提供良好的初始点，以高效获得近最优的设计方案。表4本研究和文献中的功热集成优化结果对比Table 4Comparison of integrated optimization results of work and heat in this article and literatures
本研究提出了一种基于动态运输模型的功热网络费用目标值确定方法，并采用广义析取规划方法系统性地建立了对应的数学优化模型。所提出的方法运用确定性全局算法，能够在功热网络详细设计之前高效地同步优化最佳的压力操作路径和换热匹配方案。案例优化结果得到了一种新的设计方案，得到的费用目标值结果为8761480.49 USD·a-1，相对最优性误差为5.8%，相比文献中已知的费用最优值低1.8%，验证了所提方法在最优集成下费用预测上的准确性，可以在此方法基础上结合超结构降维实现WHEN的近最优集成设计。未来的工作将进一步考虑流股的非等温相变、非线性物性方程等更加复杂的实际工程问题。Simultaneous optimization of pressure operating path and heat exchange matches in work and heat integration
ZHOU Wenjin
ZHANG YatongZHAO ZhitongZHANG Wei
（College of Chemistry and Chemical Engineering, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China）
Abstract: Traditional optimization design methods for work and heat exchange networks often first determine the pressure adjustment processes and then conduct heat exchanger network design. Superstructure-based simultaneous optimization methods for work and heat networks can achieve better overall system performance because they can consider the coupling and interactions between work and heat. However, this type of simultaneous optimization model is usually highly non-convex and non-linear, leading to solution difficulties, especially when facing large-scale industrial problems. To address this difficulty, this study proposes a deterministic optimization design method based on a dynamic transportation model. This method leverages the characteristics of the transportation model to efficiently determine the pressure operating path and heat exchange matching scheme under optimal work and heat integration. It ensures linear constraints for the heat integration model and provides guidance for the detailed design of the work and heat exchange network. A case study of power and heat integration involving 14 heat exchange streams was conducted. The proposed method generated a new pressure operating path and corresponding heat exchange matching within 1000 s. The total cost target for this solution was 8761480.49 USD·a-1, which is highly close to the cost-optimal solution found in the literature, validating the accuracy and effectiveness of the proposed method.Keywords: work and heat integration；mathematical programming；dynamic transportation model；optimal design；process system通讯作者：周文晋（1994—），男，博士，讲师，zhouwenjin@ tyut.edu.cn；张玮（1973—），女，博士，教授，zhangwei01@tyut.edu.cn
第一作者：周文晋（1994—），男，博士，讲师，zhouwenjin@ tyut.edu.cn
10个月宝宝每天需要喝多少奶粉？
